2-４　ミンコフスキー座標にほとんどの事象は書き込めない

　項目2について考えます。すなわち「光が20年かかるところを、もしそれより速い信号があるなら、20年かからずに戻る」という主張です。ここが、相対論との考え方の差が最も大きくなる部分でしょう。そして相対論の、間違いというよりも杜撰さがはっきりわかる箇所です。光が20年かかるところを、もしそれより速い信号があるなら、20年かからずに戻るということは、文句なく理に適う考えではないでしょうか。ただし、もちろん射出時点よりも後の到着時刻になるのです。
　相対論を厳密に受け止めるなら、時間をさかのぼることができるものは存在しない、ということになりますので、以下の話は全て無意味な前提で語っているということになるのかと思います。しかし私の考えは、時間をさかのぼることは時間が伸び縮みすることの一例にすぎず、ナンセンス度合いにおいて全く違いはない、というものです。そのうえでの話であるということで了解していただければよいと思います。
　一時期いろいろと話題になったタキオンという概念はもうあまり聞かなくなりました。この粒子の性質とされる、時間をさかのぼる、ということを少し考えてみると、非常に都合の悪い事態があらわになります。それは妥当性の問題ではなく、時間をさかのぼるという意味が、相対論の中で十分に意味を限定できない、ということです。
　10光年先に設置された反射板に光を当てると20年後に戻ってくるという想定に疑問をさしはさむ余地はないでしょう。そしてそれより少し遅いだけの、準光速度の信号なら21年後だったり22年後だったりに戻ってきます。では、光より速い信号は19年後や10年後に戻ると考えて、何の問題もないはずでしょう。そういう信号が実在するかということは別問題です。
　ところが相対論には、射出時よりも前の時点に戻る信号と、たとえば21年後に戻る信号はあり得ても、19年後や10年後はあり得ないのです。つまり、20年以上かけて戻る信号については、速度と戻る時間についてニュートン力学と変わりのない計算結果であるのに、突如として、射出時点から光が戻るまでの20年間が空白地帯となってしまいます。変わりのない計算結果とは、光速の2分の1の速度であれば倍の時間かかって戻り、3分の1の速度であれば三倍かかるということです。これに「およそ」という形容をつける必要はありません。視点は、地球側に置かれるからです。空白地帯が生じるのは、光速度以上になると時間をさかのぼるという概念に引っかかるので、どうしても射出時以前にもどると考えてしまうからでしょう。時間の処理を、どちらの視点で論ずるべきか、相対論に確固とした理念が存在しないのです。
　たとえば時間を逆向きに生きる猫がいるとしましょう。土の中から微細物質がわらわらと沸き上がり、毛艶の悪い、年老いた猫のかたちにまとまります。私はそいつを飼いたいと思う。でも、この猫と15年の時間を共有するとはいかなる意味なのか。食事はどうなるのか。吐き戻した餌から何かを推定して、それを与えるということなのか。後ろ向きに散歩をするのか。そもそも15年を共有できるということは、奇妙な生き物が私の時間軸に沿って生きるということではないのか。これらのことについて、かすかにでも正しそうなイメージを作れる人がいるものでしょうか。
　それとも、あるいは、逆向きの時間を生きる生物とは、無限小の時間を介してをすれ違うのみで、全く接点を作りようがないのではないか。無限小の時間という言い方に、何らかの意味を与えることができるならば、ですが。

　10光年先に設置された反射板に光を当てると20年後に戻ってくるという想定に疑問をさしはさむ余地はないでしょうし、相対論支持者も反対はしません。そしてそれより少し遅い、準光速度の信号なら21年後だったり22年後だったりに戻ります。では、光より速い信号は19年後や10年後に戻る、つまり光よりも速く戻ってくると考えることが当たり前ではないでしょうか。一つの単純な粒子と考えるから、時間をさかのぼることが可能のように思えてしまいます。しかし猫のような生き物が時間を逆向きに進むということに、正確な意味を持たせることは不可能です。
　項目2の主張を、よく注意していただくとわかります。「光よりも速い信号を送った場合、20年後よりはもっと前に戻るが、放出する現在よりは後になるだろう。決して放出時点をさらに遡った昔に戻ってくることはない」。これは要するに、光よりも早いものがもし存在するならば、光よりも先に目的地に到着するということです。

　相対論では選択肢が三つあります。通常の時間感覚側と同じ結論、すなわち20年を経ずして戻るという予想を受け入れ、ただし信号は若返っているとするか、射出時点よりも前の時間に戻ることになるとするか、ありえないことであるとして議論を拒絶するか、の三択です。
　この中で最後の「議論の拒絶」は、取り合う必要のないものではあります。ただし、もちろん相対論内部での理屈は存在します。例の式、√（1－ｖ²/ｃ²）で、ｃよりも大きい値をvに入れてしまうと、虚数になってしまうからです。さんざん数字遊びを繰り返して、いまさら虚数だから不合理という主張もどうかとは思いますが、とりあえず理屈としては通っていると言えるかもしれません。
　残りの二つはつじつま合わせの失敗にすぎず、問題のありかは同じだと思われます。通常の時間感覚の側と同じ結論を受け入れ、つまり19年後や15年後にもどる信号はあるとし、しかし信号そのものは若返っているとする考え方は、中途半端な妥協をしていると言えるでしょうか。一応言っておくと、このような考え方を取る支持者はいないと思われます。調べても出てきませんでした。ただし、選択肢としてここに書いておきます。もし誠実にこの問題を考えるなら、当然考慮のうちに入るはずだと私は思います。
　射出時よりもさらに昔の時間に戻るとする結論は、時間を信号（と同速度の移動体）視点に置くか、地球側に固定するかで混乱があります。光より速いものは時間を遡るからという、字義に拘泥すると、自然にこの考えに陥ります。つまり、光が10光年の旅をして、折り返し、地球に戻ってきたときが、光にとっては出発時と同時刻だという暗黙の定義にあくまでこだわると、すなわち20年後に戻って来てもこれが光にとっては同時刻なのであるとすると、この結果になります。問題は、このように文章化できることを、明確な形では理解せず、しかし結果として、矛盾含みのまま光の無時間性を押し通していることでしょうか。
　これが同じ仮定の話だとしても、行きっぱなしとするなら、時間をさかのぼるということを、目的地の、射出時と絶対時間で比べて過去に着くのか。それともレーザーポインタの組み立てを逆にたどって、電流となり、発電所に行くことになるのか。これでもし宇宙船がテーマであれば搭乗員が若返るなどの手段がありますが、単なる信号には適当にごまかす理屈を考えにくいでしょう。

　ではどう考えるべきなのか。私はここで因果関係を持ち出した議論にはしたくありません。つまり、射出以前の時点に戻るとしたら、既に光を受け取るという経験をしているのでなければならない、といった類のパラドックスを強調する議論は余り説得力を持たないと思っています。間違っているという意味ではなく、相対論を信ずる人がその手の理屈に心を動かした例はないという、ただそれだけの理由です。かわりに通常の時間概念の側から、この問題にわかりやすい見通しを与えておきます。相対論の支持者は、その主張とは裏腹に通常の時間概念のみによって全体を理解しているという私の考えに多少でも理があるなら、これが正しい方法だと思われるのです。

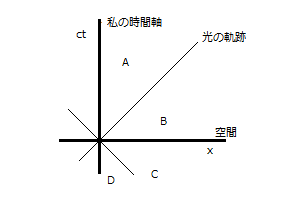
　いわゆるミンコフスキー空間を座標図は示しているわけですが、とりあえず2次元的に書き直したもので考えを進めることにします。
　これは、ある人が時空上のある位置に立ったとき、宇宙が彼にとっていかなるものかを展望させる図と喧伝されています。と言っても、別に大げさな仕掛けがあるわけではなく、y軸の代わりにct軸を置いて原点にいる人の時間線を表現し、x軸にすべての同時的空間を表現させています。図で、上に行くほど未来、そして左右に離れれば離れるほど、空間的に遠い場所ということになります。単にt（時間）ではなくctとしているのは、光が空間的パラメータと時間的パラメータを結ぶ働きをしているということの目印みたいなもので、c自体は変動のない定数ということになっているので、特にその値について神経を使う必要はありません。
　ところが、私たちはこのcに、過剰な意味づけを求めてしまいます。物理的な、すなわち現実において光が果たしている役割を、この単純な定数に込めてあるものとして考えてしまいます。現状で本当にそうなっているのか。この座標の内部で、時間は単調に推移し、空間も単純に広がっています。どうみても、それは相対論の主張とは正反対の考え方のはずです。
　まず宣言しておかねばならないことは、ミンコフスキー座標は全くのところニュートン式空間の把握法で展開されているのであって、その事実こそが、相対論的な発想では時空間を論じることが事実上不可能であることを証明する、ということです。なぜなら、相対論の考え方で座標図を展開するつもりなら、y軸がctすなわちｃ（時間）であるように、x軸はcｓすなわちc（空間）であるべきだからです。すると、原点0は静止状態にあるものではなく、光の速度で移動する者、ということになります。このことは、現段階では非常に意味のとらえがたい、荒唐無稽な主張に思えるでしょう。
　デカルト座標で通常の原点を単に空間上の「ここ」とすると、それはミンコフスキー座標では時間軸上の「現在」も意味します。これに原点から光を放った軌跡を描きいれると、上に行くほど、つまり時間が経つほど単調に原点から遠ざかることになります。ミンコフスキー座標では光速は基準となる値なので、そのグラフはct=絶対値xとしておくのが好都合でしょう。
　相対論では光が何よりも速いとされ、情報がこれを超えて伝達されることはないのはもちろん、たとえば恐ろしく長い鉄の棒があったとして、こちら側を押してやれば反対側も即座に動きそうなものですが、この押す力が向こうに伝わるにも光速度の縛りが存在するとされます。こちらを押してやったとき即座に向こう側も動く物体を仮想して「剛体」という概念を与えています。では、剛体は現実には存在しないとしても、定義としては可能なのです。「剛体は存在できないゆえに、これを使って『同時』を定義できない」と一部の学者が述べていることはどう解釈するべきなのでしょうか。実は同時的空間が相対論の内部理論ではなく、全く日常的な直観によって定義可能であるからこそ剛体というものが意味のあるものとして想像可能なのであって、その逆ではありません。同時的空間、これは相対論学者がその思想範疇にあるものとして不用意に多用する概念であるのですが、全くのところ日常的感覚にしか存在しないはずのものなのです。なぜなら相対論における同時的空間は光円錐の円錐面そのものであるはずだから。
　光円錐の意味と、表現できることは、以下のことですべてであり、それ以上のことを読み取ることも書き加えることもできません。すなわち光の軌跡というのは何かしら作用しあうということの境界線を示しているのであり、現在の私が何か仕事をすると、時間と空間の組み合わせで眺めた宇宙の中で、図のAの部分にのみ、作用を与えることができます。なお、下向きにもこのグラフは描かれておりこれは逆に現時点の私に作用を与えることのできる事象の集合を現しています。すなわち、この図の示そうとしているのは、私の近くで起きた出来事は比較的短時間のうちに私に何らかの影響を与えることができ、遠くでの出来事はそれなりの時間を経ないと影響を及ぼさないし、また、私から働きかける場合にも同様なことが言えて、その限界を光の到達速度が決定する、ということです。
　ところで、これ以上のことは表現できないという私の勝手な決めつけをとりあえず度外視してこの原則論を読み直してみるに、これは相対論とは無関係に成立するということは自明であると思います。光が宇宙の中で最高速度を持つ伝達手段であるなら、すべての物理現象は同時刻に光が到達している場所よりも近いところにしか伝播しないというのはきわめて単純な理屈であり、ニュートン力学内では成立しない、などと言えるものではありません。とりあえずエネルギーが伝わらないことには力学的な動きなど作動しようもなく、エネルギーを伝えるのは何らかの素粒子もしくは波動が相手方および目的地に行き着く必要があるはずだからです。
　それにもかかわらず、科学者たちはこれが相対論の達成であるかのように喧伝して来ました。なぜかと申しますに、この理屈がミンコフスキー座標と光円錐を使うことでようやく説明できると考えたからです。事実は逆で、今の簡略な説明で十分理解が可能であることで例証できたと思うのですが、常識的な時空間把握こそが全体を解釈する要諦なのであって、それどころか、全く不細工極まる、かつでたらめなミンコフスキー座標なるものに、どうにか説明可能性めいた外観を与えているのでした。そのうえでもう少し突き詰めて考えるなら、この外観は全くの誤解であることが明らかになります。念のために言いますと、この段階で私が指摘するのはミンコフスキー座標の間違いであって、相対論のそれではありません。
　まずミンコフスキー座標の見掛けに一つ気づくことがあるでしょう。それは、この座標の生命線ともいうべきct軸を単なる時間軸に置き換えてみると、ニュートン力学の疑似的な4次元展開そのままであるということです。立体的表現であれば3次元空間を一枚の紙のようにあらわし、それを何枚か重ねて垂直に時間軸が貫く形になります。しかしながらこの形態は相対論支持者言うところの絶対時間と絶対空間を前提とするから可能なのです。3次元空間に見立てられた一枚の紙は言うまでもなく絶対空間を表現するものであり、この形式はミンコフスキー座標においてそのまま用いられています。そうであるならば、座標の基礎的な部分で絶対空間に頼った思考に従っているわけです。もっとも、絶対時間と絶対空間という、この二つの概念に科学者がこれまで示唆してきたような深い意味はありません。単調に距離を刻む物差しと、単調に伸びる時間軸とで作った座標上にものを表現するということです。つまりミンコフスキー座標そのものの姿です。
　これは先回りの安易な批判に思えるでしょう。しかしいずれにせよ相対論の建前にミンコフスキー座標が応えきれていないことは事実だと思われるのです。ニュートン力学の疑似的4次元表現はニュートン力学を十全に表現しています。言うなれば、座標のパラメータは、私たちがこれを直感的に把握するそのままの姿です。座標上の短い距離は近い距離、もしくは時間的な短さを表現しています。ミンコフスキー座標はそうではありません。座標上の短い距離が時間上はより長い時間を表し、あろうことかこの齟齬具合を自慢します。
　そもそも、座標やグラフを使っての表現とは、複雑すぎて把握の難しいデータ群や現実の一側面を直観的に見て取れるようにする工夫です。デカルト式座標があたかも現実そのものの断片に見えるということは、言うなれば私たちにとって大変幸福な偶然ですが、大切なのは直観的な把握が可能であるという部分だと思います。しかるにミンコフスキー座標はこれを眺める人に直観的な理解を許しません。学者は例によって理解の難しさを現実の複雑さ、あるいは読み取る側の頭の悪さに帰結させるのですが、学者自身も全く理解できていないことは、この図表の解説がどれもこれも相対論の数式との突合せに終わっており、たとえばパラメータの表現の不具合を十分に説明できないことなどからも明らかではないでしょうか。
　それが直接に相対論の反論にはならないとしても、この図表があまりうまくないことは確かです。ここまでニュートン力学を表すのに適した座標が、全く別の思考形態にぴったりはまるわけがありません。なぜならこの座標において時間も空間軸も等間隔の刻みで単調に伸びる形になっているからです。いかなる意味においてもこの二つに単独で正確な量を与えることはできない、ということが相対論の建前でした。したがってこの理論に忠実であるなら、等間隔に刻まれた目盛りが振られるべきは光の軌道のみであるはずなのです。
　ミンコフスキー座標が相対論の建前を表現できていないだけなのか、もともとこの不完全さが相対論の性格そのものなのかは、ここまでの考察からは明らかになりません。しかし、学者が建前を十分表現できたと認める座標が存在しうるとして、それがどのような形になるのかは私にはわからないところです。そしてもうひとつ、学者たちはこの座標図をもとに気ままな空想を広げているのであり、当然ながらその空想は根拠を持たない言いがかりとして排除されなければなりません。私が排除するのではなく、本来ならば相対論支持者の方から批判が起こらなければおかしいということです。
　説明可能性の見掛けを、相対論の主張に沿って考えてみましょう。いくつかある主張の一つが、この座標にある位置が描きこまれた場合、それは「もの」ではなく、ある「出来事」だということです。たとえば任意のp点があったとして、それは大マゼラン雲の位置を示すのではなく、宇宙船が大マゼラン雲に到着したとか、私が初めて大マゼラン雲を見た、などという事象を示します。そしてその事象は私とかかわるものでなければなりません。なぜなら私とのかかわり方によってはじめてその事象の時間が決定できるからです。例えば、本当に適当に二つの点をAに描きこんで、その二点を結び、生成（b）から消滅（a）までの軌跡とすることで、ある天体の生涯を書き込めるような気がします。
　しかし20歳の私が一億年とみなす生成から消滅までを30歳の私は八千万年とみなすかもしれません。時代を隔てた私は、その星との相対速度を変化させているかもしれず、その場合にその星の寿命も異なるものとして把握することになります。すなわち生成から消滅までのプロセスは中心の時間線すなわち私のどの時点とかかわりを持つかによって全く違う意味を持ちます。線分abの内容は、ct軸上の（例えば）mから見るかnから見るかで変化します。ところが、かかわりの持ち方とはいかなる意味なのかそもそも不分明なのです。私の側から生成の瞬間をめがけて何かの働き掛けをするということはまずないでしょう。一般的には、目撃する、すなわち光を受け取るということになると思います。では星の一生などという長期間のものは正確には描けないはずのものなのです。
　ここでありうる反論は、この図全体が原点における私の速度、ひいては私の時間の流れをそのまま延長することを前提としたものであるから問題ない、というものでしょうか。それはつまり、原点における私の速度、ひいては時間の流れをそのまま延長することを前提とした全体の記述が可能であるということになります。この反問は一見無意味でしょうが、私が言いたいのは、そのような全体の記述は物理学として不完全であるという主張が相対論の側の取柄だったはずだということです。いま申しました「原点における私の速度、ひいては時間の流れをそのまま延長することを前提とした全体の記述が可能である」ならば、ニュートン力学が可能だということになるのではないでしょうか。そしてそれは今まで繰り返した通り、さらにこの先明らかになる通り、相対論よりはるかに包括的で柔軟な思考なのです。

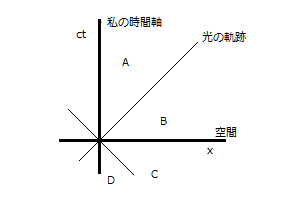
　基本図を再掲いたします。相対論で時間論を展開すると、日常の感覚に沿わないことが次々に出てきますが、そもそも相対論の定義する過去、未来と、日常概念のそれとはかなり違いがあります。日常概念ではx軸より下の部分は過去になります。作用可能性で定義できる時間、および光速度で考えられた相対論の時間概念ではAのみが私の未来世界です。Dはどちらの世界観でも過去になるけれど、Cについては多少怪しいでしょう。通常感覚ではもちろん異論の余地なく過去ですが、相対論ではこの部分が意識して論じられているわけではないのです。図面上では存在しているはずなのに、理論的には定義不能であり、議論にも上りません。
　理論的には定義不能、と書きましたが、実は明快な定義が可能です。ただし、学者がそれを認めることはないはずなので、それを承知の上で書くことにいたしましょう。Aについて言うなら、それは「原点から遠ざかる動き」という意味があります。遠ざかるとは、時間的空間的、ともに含むものです。この部分に点を打つなら、それは直線的に遠ざかる信号の4次元的表記の一断面を示すことになると思います。ただしこの4次元的表記とはニュートン式の疑似4次元です。
　Bは絶対時間では未来でありながら、光円錐による時間感覚では過去になります。つまりそこに存在する事象に対して働きかけはできません。しかしもしそれが、たとえば超新星の爆発であるなら、いつかはその光を受けることができるという意味で過去にはなりえます。また、現実には存在しないかなり過去の私なら、働きかける可能性もあったという意味で、過去の事象と言えます。Dは近づく動き、CはBと同様の非常にあいまいな領域ということになるでしょう。認識上は過去に属しながら、原点の私になんらかの作用を与えるためのシグナルを送ることができない部分です。ただし私の未来に影響を与えることは可能なので、相対論支持者のさまざまに入り組んだ作り話の中では未来として語られます。
　つまりB、Cはよく整理されないままその時の話の都合で未来にも過去にも分類されてしまうわけです。タイムパラドックスのような、一見解きほぐすことのできない謎は、この部分をきれいに整理すれば生じないはずでした。言うなればニュートン式の絶対時空間と相対論の建前である光円錐に基づく時間とを無頓着に混ぜて使う支持者たちの態度がもたらしたものです。しかし後者の建前のみの時間論一つに頼って宇宙を論じることは私見によれば不可能でしょう。
　B、Cの正確な意味を学者が認めるはずがないと書きましたが、ここでもまた多少の訂正をいたします。ワイルが例によって先鞭をつけているからです。彼はAを能動的未来、Bを受動的未来と名付け、t=0は客観的意味を持たないのであって、時制のすべては作用によって定義されると言いました。この大変もっともらしい趣向に人々は騙されたわけです。つまりいかにも深い意味がここにあるような気がしますが、同時刻は意味を持たないと言い放ったうえで、時計をいちいちその同時刻の地点まで運んで同じ時刻であると追認しているのであって、それならば同時刻は意味があるのです。もう少し後で、相対論支持者の言う「作用による定義」が通常の時空間概念をもとにしていることを論じますが、とりあえずここでは、主観的客観的とはそれこそ意味のない形容であって、主観的に意味があるなら客観的にも意味があるのであり、作用によって同時刻の位置が決められるなら、当たり前ですが別の方法でその位置を確定しても無意味にはならないと言っておきます。
　おそらくワイルは客観的意味を持たないという言い方で絶対時間は存在しないということを表現したかったのでしょう。これが無意味な罵倒語にすぎないことはたびたび繰り返しました。時計を移動させることで追認できる同時刻をいろいろな考えの基準とすることは可能であり、大変現実的な戦略であると思います。それを絶対的時間と呼ぶかどうかは本質的な問題ではありません。
　光円錐の意味が通常概念で十分に分析可能であるのに、相対論のみがそれを明らかにするというもっともらしい作り話が簡単に信じられてしまいました。同様に、ミンコフスキー座標内の出来事は通常概念で理解可能であるのに、いちいち相対論の理屈で上塗りされます。
　作用とは何か。自然界は多様であるから、いろいろな内容を考えることができるでしょうが、とりあえず力が伝わるその軌道を座標上に示すことは、一つの物体がそちらへ向かうことと区別できないのですから、私たちはもっと単純な見方を選ぶべきなのです。作用という複合的な概念ではなく、物体の移動と考えるべきであるとすれば、この座標上では描かれた物体は必ず移動しなければならず、しかもctとcという時間の方向付けによってこの図表全体ががんじがらめにされており、結果としてきわめて単純な動きしか書き込めません。事実は、原点から単調に遠ざかる動きと単調に原点に向かってくる動きの二通りしかミンコフスキー座標上には存在しないのです。もっと複雑なさまざまのことをここに表現できるというのは学者たちの勝手気ままな空想にすぎません。