2-7　無限大ということを現実世界の中で考える

　ポアンカレ運動に対しては、主に二つの点で批判ができますが、無限大の速度という概念に深くかかわるほうから考えてみることにします。

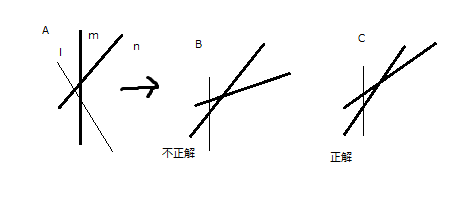
　上図でまずmの視点で見ていたものをlの視点に書き換える際、mとnの成す角度、つまり速度差は、A図のままが維持されるBではなく、Cが正解です（図が下手なのでわかりにくくて申し訳ありませんが）。すなわち同じ速度差を表現するのはより小さい角度である必要があります。もしかしたら相対論では実際に速度差が小さいという表現になるのかもしれないけれど、要点は同じで、ここには描かれていない水平軸に近づくにつれ同じ速度差でも小さな角度で示されるということです。「実際は同じ速度差だが小さいものとして表現される」と「実際にも小さな速度差なので小さく表現される」は図と現実の照応関係に対する二通りの解釈であって、奇妙なことですが、図そのものはどちらも等しく支持していると考えることが可能です。つまり図の「文法」の正しさはどちらの内容であるかに依存せず、ここでの私の批判はその文法に対するものであって、現実に対する解釈の違いではないのです。図の規約に関する当否は当然純粋に理論的な問題なので、現実がどうあるかという問いとは無関係に決定できます。

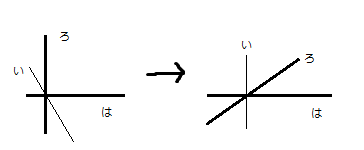
　極端な例で考えるとして、「は」は「ろ」に対してほぼ無限大の速度で遠ざかっています。つまり「は」は座標軸ではないのであって、したがって垂直に交わっているわけではありません。それを右のように「い」の視点で見た場合、「は」の世界線は全く変化がないように描かれます。もし「は」の向こうにやはり「は」からほぼ無限大の速度で遠ざかる世界線があったとしても、やはり「い」の立場から見て「は」と重なるような描き方をされるでしょう。ここから言えるのは、以下の図において、右図矢印のような角度の信号はありえないということになります。

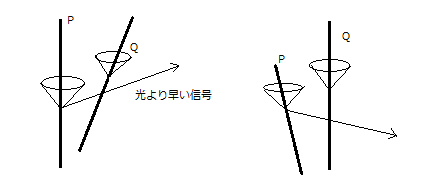
　これはミンコフスキー座標を想定しているにもかかわらず、図を描く段になって単純にデカルト座標的なとらえ方をしていることからくる錯誤でしょう。なお、ここまで述べたことについて、ほぼ無限大の速度というとき、ニュートン力学上のほぼ無限大と、アインシュタイン力学内での事実上のほぼ無限大とで、図の中での確認事項について、なんの違いもありません。
　ここで一つの解釈があります。それは上図の右の信号は矢印の向きではなく、それとは逆に、Pのほうへ向かっているものとしてQの立場からは見える、という考え方で、たとえばペンローズなどはそう述べています。この意見の背後にあるのは、もとは至極まっとうな見方であるにもかかわらず相対論の中でいつも勘違いとともに応用される日常的事実です。
　近づいてくる乗り物があり、そこから路傍の私に向けて乗り物より遅い信号が発せられているとしましょう。私が乗り物を視覚できず、信号だけに着目するなら、乗り物は遠ざかっているように見えます。

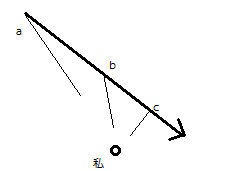
　図のa、b、cそれぞれから私に向かってゆっくりとした信号を送るとして、もしこの乗り物がきわめて速く移動しているなら（できるだけ極端に考えて、1秒でaからcまで動く、そして信号はaと私の間で分単位の時間がかかるものとするとわかりやすい）、私が最も早く見ることになるのはcからの信号で、次にbからのものになります。つまりこの乗り物がcからb、aとたどっているように見えることはタイムパラドックスや空間のゆがみなどを持ち出さなくても日常感覚のままで肯定できます。
　この、矛盾とは感じないという時空把握のあり方がミンコフスキー座標の中でも生きています。矛盾にならないのは、「実際には」と問うことが通常感覚の中では意味を持つからです。つまり上に掲げた乗り物の例のごとく、逆行しているように見えることがあるとしても、実際には常に順行状態であるという答えが存在します。ミンコフスキー時空の中では、矛盾はないという感覚のみ暗に主張され、しかし逆行は事実であることになってしまいます。むしろ、順行も逆行もともに事実であると認めたがっているように見受けられることさえあります。
　光が或る場所から別の場所へ移動する同じ経路を、別の光は逆向きにたどることができます。だとしても、それは同じ光ではありません。ここに可逆性があるかのように論じてはいけないのです。ペンローズなどの意見は、経路を単純に切り取って時間的な対称性が存在するかのようにみなしていますが、光を発射するまでに、たとえばレーザー装置を設置するだとか、発電所からケーブルを引くだとかの作業もあるはずで、光が逆行すると主張されるとき本来ならばその部分まで経路に含まれるべきなのです。その部分まで経路に含むなら、時間的対称性を持つ物理現象など宇宙に存在しない、という結論が妥当であると考えられるでしょう。可逆的な現象と思われることは、そう論じられる部分を都合よく切り取っているにすぎません。もっと広い切り取り方をすれば必ず非可逆性を持ちます。宇宙に起きたすべてのことはその意味で可逆的ではありえないのです。
　ここまで述べて来ると、遠くの銀河では時間の進みが遅いはずであるということとの類似性が明らかになります。つまり、地球外のある視点から私がレーザー光を操る様子がフィルムの逆回しのように見えることが仮にあるとしても、私自身には全くその感覚はありません。感覚はないが実は時間が逆転しているはずだと主張するのはナンセンスだと思われます。

　カントールの実無限と、それに反対を唱える可能無限との立場は何かというに、手の上で自在に無限の観念を扱い、それが計算可能な定数にすぎず、あまつさえその外に出てこれをながめることができるかのような立場をとるのが実無限であり、決して到達可能ではなく、計算の対象ともなり得ないというのが可能無限ということになるでしょうか。
　ポアンカレ運動とは、無限大を超える速度が存在し得る場合に、情報を過去に送り届けることが可能になるという理屈です。無限大を超える速度はあり得ない、と私たちは直観的に感じるでしょう。それは必ずしもニュートン力学を採用するから、ではありません。そもそも無限大の速度すらあり得ないと思われるのです。
　ところが相対論では光速度を「名目上の無限大」として処理するので、それを超える速度が考察の対象になりうるのです。もちろんこの点でも、当たり前の感覚では「光速度は無限大ではない」ということになるはずですが。
　ふしぎなことに、カントールの提唱する実無限の集合論と、相対論の名目上の無限大とがここで重なって見えてきます。現実世界において、無限大であるところの何かには到達しえません。無限とは可能性にとどまるという意味で、それは可能無限でしかありえないのです（もちろんビッグバンやブラックホールを信じる側からすると暴論になることは承知しています）。無限大の速度と私たちがいうとき、同時というものを無理やり到達速度の側から解釈することによるのであって、速度よりも時間のほうが根本的な観念であるからそもそも時間が速度を基礎づけるのであり、逆はあり得ないと思います。したがってここで無限大とは、概念空間のみで使用しているのであり、現実的である必要はないというニュアンス込みで言っております。
　実無限集合論の根拠である無限小数には、はっきり定義できるもの（√で表現する数や円周率など）と、はっきり定義できない、無限小数としか呼びようのない、正体不明の実数がありますが、同じものとして扱われます。後者は有理数であるか無理数であるかさえ定かではなく、量も確定できず、計算もできません。要するに、実無限が正しいと主張するためにのみ作られた、対角線論法という場だけに現れる架空の数字に過ぎません。無限の濃度の違いは、無限の性質を表現しているのかということは、多少の疑問を残します。
　カントールの集合論も相対論も、無限大よりも大きな量を想定し、無限大の量があたかも部分的な量のごとくに語ります。つまり無限とは名目上のことになります。だからそれを超える何かが想定できてしまう。これは矛盾などと言うしゃれたものでは全くなくて、単に言葉（数学的操作）によるごまかしではないでしょうか。

　次に、私にはより重要だと思われるけれど、哲学的であるため納得しがたい人が多いであろう論点を考えます。何らかの形での過去への行き来を可能にするのは、ペンローズ言うところの同時的空間の傾きということになります。要するに時間と空間のゆがみのことです。矛盾含みであるはずの概念でも、場合に応じて二通りの表現が与えられ、それぞれがその属するカテゴリ内ではある程度の妥当性を持つとき、深く追及されることなく納得できてしまいます。相対論には、わざとかどうか知らないが、そのような例があまりにも多いようです。ポアンカレ運動の主張は、恐ろしく遠くにある星、たとえばかみのけ座銀河団の一惑星から地球へ向けて使節が派遣されたとして、Aにとっての同時的空間はその使節団が出発前の状態であっても、Bにとっては出発後のことかもしれない、ということを導くことができます。もしもここで時空の構造がAにもBにも正当に主張できる形でゆがんでいるのだとするなら、並行宇宙論を採用しているか、視点の切り替えでたちどころにはるかかなたまで影響を与えるような不可思議な方法で歪みが実現されるのかでなければなりません。
　おそらくここで並行宇宙論という強い抵抗を持つ表現を使ったがゆえに即座に否定したくなるでしょうが、Aから見た場合とBから見た場合に宇宙自体は全く別のゆがみ方をしており、それがどちらも成立するということは、もし単なる個体同士の関係であるという前提を最初に退けるなら「単に、そのものに対するいろいろな見方がある」と言うか「まったく別の構造として存在している」と言うかの二択になります。しかし相対論が、前者が意味すること以上の深刻なニュアンスを持たせたがっていることは間違いないのです。なぜなら、いろいろな見方がある、とは、結局のところ個体どうしの関係にすぎないと言うに等しいからです。したがって、相対論では、心理的に抵抗のない表現で多元宇宙論を支持している、と結論するべきなのです。
　今の最後の文はすぐには直前の文章につながらないと感じるでしょう。真意はどこにあるのか。時空がまがると言うとき、そのまがった中にあるものは、実際に物理的な影響を受けているのでなければなりません。AとBのすれ違いがかなり極端な速度で実行された場合、かみのけ座銀河団の受ける時空のゆがみの事実も、かなり違うものになります。この場合、ゆがみの実情を後から確認して「あれはこうこうであった」とする情報論の形を、相対論は求めていないはずでした。すなわちAとBがすれ違った時点で、すでにかみのけ座銀河団の時空は各自に対してゆがんでいることが、この理論の主張です。もし地球と銀河団との中間に大きな天体があったとして、この天体は遠く離れた場所の高々数十キログラムの物体のことなど全く関知しないでしょうが（笑ってしまうほど微弱な重力の影響はあるにしろ）、それでもABがかみのけ座銀河団に注目したおかげで、おおいに時空のゆがみの犠牲になる羽目になるのです。
　また、物体同士の関係は近ければ強く、遠ければ弱くなりますが、大変奇妙なことに、空間のゆがみは遠いほど大きくなります。いろいろ反論したくなるでしょうが、時空がゆがむとは、そういうことではないでしょうか。曲率kの空間があるということは、ある物体が曲率kの軌道を描いて移動するということとは違い、あらかじめゆがんだものとして物体が来るのを待ち構えているということです。これを否定したくなるなら、なぜ「ある物体が曲率kの軌道を描いて移動する」という表現を使わないのでしょうか。それはもちろん空間のゆがみというイメージが何かを説明しているような気がするからなのです。しかし空間のゆがみがあらかじめ物体の到着を待っているとすることはできません。相対論に従う限り、そのように無限大の速さを持つ物理的な力を考えることはできないからです。だからと言って、移動する物体がある領域に到達したとき、はじめてその領域のゆがみが開示されるということであれば、もはやそれを時空のゆがみと呼ぶ必要はありません。物体がそういう軌道を描く、と言えばよいのです。