二人に区別をつけるために、私と友人ということにしておきます。私には友人と呼べるような人物は存在しませんが、とりあえずの話です。相対論の時空概念は矛盾しているので、あちらもこちらも正確に表現するということはできません。時間か空間のいずれか、あるいはほかの部分にごまかしを仕込むということになります。しかしいったん絵にしてしまうと、いかにも筋が通っているように思え、それに対する私の説明のほうが間違っているようにとられかねません。世の中にはたくさんの相対論解説書がありますが、いずれも必ずごまかしを含むということは覚えておいてよいでしょう。おそらく同時的空間を説明する際、相対論支持者の説明図は以下のようなものになると思います。

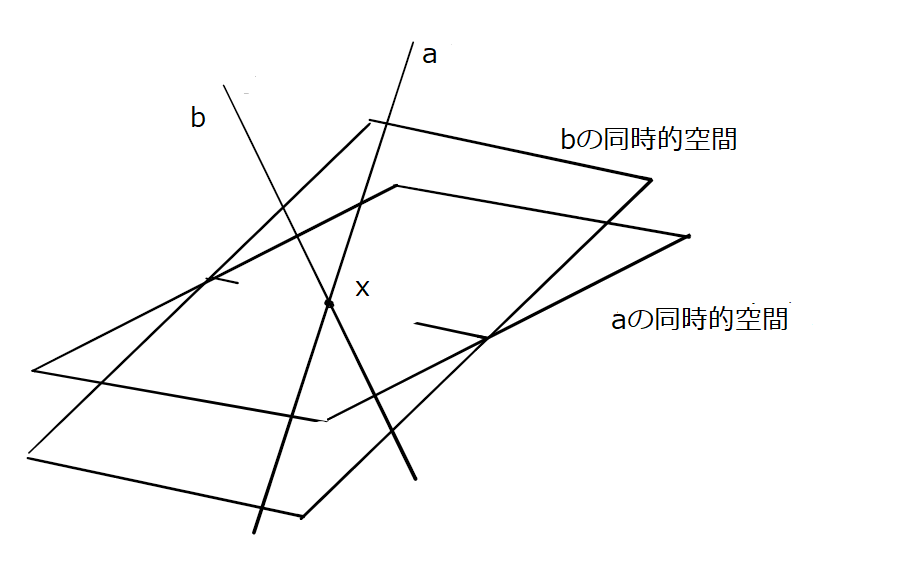
　2本の世界線を交差させ、その一点にそれぞれの同時的空間を適当な角度をつけて描くと、遠くに行くほど広がる形になるので、いかにも正しい主張を聞いた気がします。しかしこの説明図は明らかに間違っているのです。なぜなら、わかりやすく説明するための当然の設定として、地球とアンドロメダ大星雲の距離は変わらないことになっており、したがって時間の進行速度に違いはありません。そうであるなら、あちら側で数週間のずれが生ずるとしたら、すでに地球側でも同じ大きさのずれがなければならないからです。
　第一感は、私のこの意見のほうが間違いであるということでしょう。現実に地球で数週間の時間のずれなどという事態を目撃することはできないし、遠くでそのずれは増幅できそうな気がしてしまうからです。
　ペンローズはおそらく相対論中のいずれかの式を当てはめてみただけなのでしょうから、具体的な考えをたどることはできにくいのですが、一例として次のような思考経路はありえます。ただしこれはこの通りに考えたということではなく、計算したことの意味内容が結果としてこうなる、ということです。
“私がレーザーポインタを向けた時点の同時刻を求めるにあたって、光が大星雲に届いた時点から230万年さかのぼることにする。しかし大星雲と私は時間の進み方に差があり、その場合に、運動体である私のほうが進行は遅いことになる。したがって、230万プラスアルファさかのぼった時点が同時刻である。”
　しかし逆に230万プラスアルファさかのぼった時点にあちらから放たれた光は、私がこちらで光を放つ瞬間に届くのではありません。プラスアルファの、そのアルファ分だけ前に届いています。なぜなら地球にはすでに届いているのであり、その地球対私の間で、大きな時間のずれなど目撃できない、ということがはっきりしているからです。相互関係が成立していないので、私の光放出の瞬間と、それがあちらに届いてから230万プラスアルファの瞬間は、同時刻ではありません。
　光速度不変の原理を守るなら、速度による時間の進み方の違いということは成立しないのです。相対論において時間のずれは方向性を無視した単純な速度で決定されますので、私、友人、アンドロメダ大星雲の三者が別別の速度を持つだけで条件が満たされるはずです。したがって例えばアンドロメダ大星雲を中点とする巨大な球体の表面で私と友人の歩みが交錯する形、すなわち二人は常にアンドロメダ大星雲から等距離にあるという図でも、同時的空間の傾きは生ずるということになります。

　二つの矢印の起点と先端において、大星雲からの光の到達時間はどちらも230万年であって、このことはaとbの長さの如何にかかわらず、すなわち速度の大小にかかわらず同一です。片方が歩く速度、もう一方がほぼ光速度であっても、やはりベクトルの始点と終点において、そして道中のすべての時点で、光は同じ時間を費やして届きます。同時的空間の傾きなど生じようがありません。ペンローズなどの主張は、二つのベクトルの交錯点においてのみ光の到達時間が一致し、ベクトルのほかの部分では変わるという漠然たるイメージを含むものであると思うのですが、この図のような距離関係においてそのことは成立しがたくなります。すなわち交錯点がアンドロメダ大星雲からの光を同時に受け取るのであれば、ベクトルの始点どうし、先端どうしにおいても同じ瞬間の光を受け取るはずなのです。二つのベクトル上のいかなる時点においても、アンドロメダ大星雲から発する光、そして私と友人がそちらへ向けて発する光は同じ時間をかけて、同じ距離を移動して相手方に到達します。
　その意味は、三者にそれぞれ時計を持たせたとして、その進行は常に同期するということです。これは絵にかいたごとく相対論の同時刻についての定義にかなった相互チェックが常に可能な状態であり、時間の伸び縮みが入る余地はありません。すなわち、運動状態は時間の進行速度に影響を与えることはできないのです。

　ところで、アンドロメダ星雲を取り囲む大球で考え得たことは、そっくりそのまま地球をめぐる衛星にも応用できます。つまり地上から衛星までの高さを考えるのではなく、地球の中心からの距離という考え方を取るのです。わかりやすくするため、モデルに頼ってみましょう。小さなステーションを中空に設置し、そこを中心に15万㎞の位置に複数の衛星を巡らせます。衛星の速度はそれぞれ違うものとします。
　この衛星は非常に特殊な時計を積んでいます。光をステーションに向けて放つと、それはおよそ0.5秒後に到着し、するとステーションはその衛星に向けて光を投げ返す。衛星がそれを受け取った時点を振り子の一往復とみなし、全体の工程を1秒に設定します。これはもっとも相対論の原理に忠実な、正確な時計のはずです。ファインマンが光時計というものを夢想したように、根本原理である光を使って時間を計るということが、相対論の理想なのですから。
　すぐにわかるように、衛星の速度がどうであろうと、時計の進み方は同じです。すべてがステーションの時間の進みに同期するので、それは当然でしょう。では、本当は衛星ごとに時間の進みが違うのに、無理にステーション基準の時間を当てはめているということになるのでしょうか。
そうではありません。相対論の論文も、あるいはヘルマン・ワイルのより数学的に洗練された理論でも、それぞれの場所に時計を置き、その同時刻のチェックということに光の信号を使っています。これによって、それぞれの時計が固有の時間を刻み、しかし光信号によって相互チェックは可能であるという漠然とした印象を人は持つことになります。しかしよく諸論文を読めばわかるとおり、時計が刻む固有時間より、光信号のチェックが正しい。時計の存在はただ「それぞれに固有の時間の流れがある」という印象を作るために使われているのです。ならば話は簡単で、衛星に適当なゼンマイ時計を積めばよい。そしてそれを1秒周期の光のやり取りで厳格に調整します。これで相対論関連の諸論文に見る、同時刻の定義にかなう時間計測システムになります。
　ここから導かれる結論は、衛星の速度がどの程度であろうと、時間の進みに差はない、そしてその時間の進みは地球のコアとも同期するのであって、したがって地上の時計とも同期する、となるでしょう。つまり相対論の枠内で思考するとして、光速度が一定なら時間は伸び縮みしないし、時間を可変的とするなら光もそれにかなう相対速度を持つことを認めるほかはないのです。