2-8　光時計という空想

　ここまでの要旨は通常の時間概念における過去、未来と、相対論による過去未来との間に食い違いがあり、相対性理論の側こそが実はその違いをうまく把握できていないということでした。相対論の時間概念は本当のところ通常の時間感覚に全く依拠しきっており、せっかく独自の定義を与えながらそれを守ることができていません。従って通常感覚の時間と相対論的時間との違いを見逃しています。
　ここでもう一度出発点でのパラドックスを確認しておきます。高速で動くものはその外で静観する私たちに比べて時間の進みが遅く、進行方向に対して長さが縮み、かつ質量が増す。これを相対論の相互的であるべきという要請に従って考えるなら、その高速で動く側から見るとき私たちのほうが時間の進みが遅くなり進行方向に縮み、重くなるということになります。そして主流の科学者の意見では、私たちに時間の遅れその他の自覚がないのは、たとえば単に主観的な見方にすぎないからということになるのでしょうか。つまり事実がもともと矛盾含みのものであるのだから、それに文句をつけるよりも自然の不思議に讃嘆しておけということになり、じっさいに科学者は相対論の不思議な帰結を手放しで宇宙そのものの神秘としてきました。
　ここまであからさまなパラドックスを内包した理論は、間違っている、とすることがもちろん最良の選択でしょうが、奇妙なことに科学者はこれをかたくなに拒否します。では、このパラドックスに対し納得のゆく回答を与えるのでなければなりません。たとえば速度によって質量の増減があるとして、銀河系に対して光速度以上の相対速度を持つ、いわゆる時空の地平線外の領域が存在する以上は、そこの住人からすると私たちこそが光を超える速度で遠ざかっているわけなので、この地球ですら無限大の質量をもたねばならず、したがって私たちはブラックホールの内部に生活しているとしても間違いはないはずです。なぜそうなっていないのか。自覚がないだけと言って済ませられることなのか。もしこれを空間の広がりと内容の移動速度とは別物だとして回避できたとしても、一般相対性理論の提唱する等価原理、すなわち重力と空間の加速度とは完全に同一視できるものであるとする考えを援用するなら、現実に存在するとされるブラックホールたとえば白鳥座xは加速度状態にあるわけであって、そうなるともしそのブラックホールから見た場合、わが地球が逆の加速度状態に置かれるのでなければならないはずでしょう。つまりいずれにしても現実にブラックホールがどこかに存在しうるなら地球がブラックホールでなければならないという奇妙な結論を導くことができます。だがその特異点はどこにあるのでしょう。白鳥座xから見た場合は、宇宙のすべてが特異点ということが結論なのかもしれません。
　この言い分をおそらく多くの人は奇妙な思い付きと切り捨てるのでしょうが、もちろんそれは回答になりません。もしかしたら誰かが答えを出しているのかもしれませんが、私は未聞です。宇宙全体がブラックホールの内部にあり、実際に現在は内部に崩壊しつつある過程である、という本を見たことはありますが、どの程度に信じられているのか、心もとないところです。そのほか、ありていに言って、疑問を感じる者が科学に無知であるとするか、自然とはそういう不思議なものだと開き直るか、どちらかの回答しか提出されてこなかったと思います。多くの人がこれで納得できているらしいのはいくらなんでも異様なことではないでしょうか。
　では逆に考えてみましょう。なぜこのパラドックスに答えるべき真実があると私たちは思わされるのか、つまりなぜここまであからさまなパラドックスを内包した理論を即座に切り捨てないのか（私たちは、という主語は偽善に映ります。なぜなら､私はこの理論を信じないから。しかし説明すべき何かがあるとは感じます）。また哲学的な、というより心理的な物言いになりますが、私の考えではこれは純粋に理論上の出来事であるがゆえに回答が可能なはずであり、納得できる見方が今まで出されないからこそ答えられるべきであると感じるのです。つまり単なるパズルなのです。パズルであるなら、もし回答が存在しない場合に作者のミスであるという究極の回答も含めて、必ず解けます。もし納得できる解決、その最悪の場合でもなぜ作者はミスしたのかという疑問への回答が存在するなら、その時こそこれを受け入れるか捨て去るかの判断が可能になるはずなのです。

　時間論だけに的を絞るなら、相対論のもたらす矛盾はいわゆるウラシマ効果と双子のパラドックスに典型的に表れます。ウラシマ効果とは、その言葉通り、浦島太郎の昔話を相対論によって再現することです。二十歳の双子がいて、弟は地上に残り、兄が地球の時計換算で十年がかりの宇宙旅行に出かけたとする。再会の折、たとえば弟は30で兄は25である、という状況がありうるとするのが、相対論の言い分でした。年齢がこのような数値になるものかどうかはともかく、これはすでに常識的な見方の一部であるとされます。要点は、地球にとどまる弟は、移動する兄より必ず早く年を取るということです。これを可能にする考え方は相対論が時間のゆがみを肯定するという解釈から来ています。

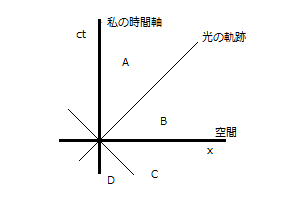
　上にもう一度基本の図を掲げます。これはもし本当ならデカルトの空間座標が3次元的に描かれるべきであるように、4次元のものとして描かれるはずなのですが、極端に省略して平面にしたミンコフスキー座標です。科学の解説書などに出てくる図は同じ省略形でも多少立体的に見えるような描き方をしています（たとえば光の軌跡は漏斗状になっている）が、どっち道正確に描くことは不可能なのだから、ごまかしと言えばごまかしでしょう。なぜなら3次元のデカルト座標はもし立体透視で描くならほぼ事実通りになります。つまり2次元のデカルト座標は現実の断片そのものですが、ミンコフスキーのそれは断じてそうではありません。ミンコフスキー座標を、たとえば無数の立体図を用意して、時間を追ってぱらぱら漫画のように見せることにしても事実の通りになることはないのですから。
　二つの座標図の、何が一番違うのでしょう。3次元空間のデカルト座標において、任意の一点Pまでの原点からの距離をSとすると、それはS²=x²+y²+z²を解くことで与えられる、単純な空間的へだたりを表します。ミンコフスキー幾何学では同じく任意の一点Pまでの距離はS²=x²+y²+z²－c²t²と書かれ、これは原点からPに至るまでに要する時間であるとされます。

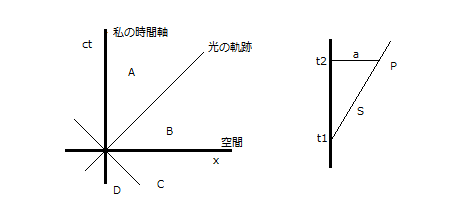
　混乱を招くだけだからあまり寄り道はしたくないのですが、ミンコフスキー図の解釈において、学者の言い分に相当譲歩した形を取らなければ先に進めないことをまず確認しておくべきでしょう。任意の点というのは、先に書いた通り、場所を指すわけではなくある事件を示します。といたしますと、本当のところある時間的幅を持って運動状態にあるものしかこの図の中に描けないことになります。上図右は時刻t1に宇宙船が地球を後にして、それがaの距離にまで達したとき、地球にいる私にとってt2－t1の時間が経過していることを示します。ところで、先のミンコフスキー方程式をここで使いたい場合、この図ではyとzが省略されているので、S²＝x²－c²t²と考え、さらに置き換えてx²－S²=c²t²とすると、いずれの項も正であるので、t2－t1は常にSより大きい、すなわち地球に残った私の時間経過は、宇宙船のそれよりも大きい値になることがわかります。これは引かれた線分の見た目とは逆の関係であり、つまり長い線分ほど短い時間を示すので、なかなか合点のゆかないことです。なぜそうなるかということについて、学者が正確な説明を提供したことはなかったと思います。なぜなら彼らも理由がわかってないからです。なぜわかってないと決めつけることができるのか。それは再掲図1のA領域に、過去に起きた様々の事象を描きこむことが可能だと彼らが考えていることから察せられるのです。いくつかの宇宙論の書物を参照していただけるならばこのことが裏付けられるでしょう。
　きわめて単純な錯覚があるのです。それは、光の時間は0であるとされていることに起因します。

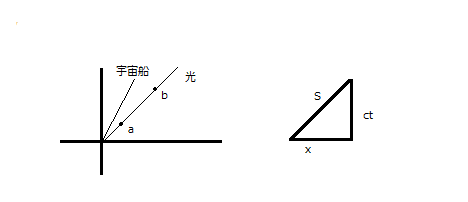
　上図において光の場合aからbへ至る間の時間経過はないものとみなされます。これは今まで繰り返してきたとおりのことです。上の右図を見ればすぐにわかるように、ここで使われるパラメータの組み合わせは光の軌跡を斜辺とする直角二等辺三角形になるのですからctとxは等しい。これを二乗してピタゴラスの定理のように足し算するならともかく、引き算をする（S²=x²－c²t²）のだからS（要するにaからbまで）はいつでも0になるに決まっているのです。このような帰結を十分に想像してミンコフスキーの式が作られているのでしょうか。どちらかと言うと、式だけが作られ、機械的に運用してみたら光が無時間になってしまったというのが本当のところだと思われます。もちろん原点にいる私が光を放つなら（左図）それは一定時間後にaに到達し、そののちbに到着するでしょう。それは縦軸の私の時間としては勘案されますが、光はその時間の流れに取り込まれないのです。このこと自体の理不尽さはすでにふれたので、とりあえずそういう世界観もありうるとしておきましょう。おそらく光は運動するものとしてではなく、世界の境界面としてぼんやりととらえられているのです。
　しかしたとえば木星と火星に偶然同時に彗星が衝突したといたします。これを観測する私はまず火星の光景を見ることになります。彗星の火星との衝突はその時過去に開かれた光円錐の上にあり、木星への衝突は光円錐の外にあります。しばらく経過して木星への衝突を見るとき、今度はこちらが光円錐上の出来事であると認識されます。火星への衝突は光円錐の内部での出来事になるでしょう。つまり宇宙の出来事のすべては、一度は光円錐上に、すなわち時間のない世界におかれます。時間のない世界におかれたのに、何ゆえ次の瞬間時間の中に巻き込まれるのか。私が時間に巻き込まれるから、ということは回答にならないでしょう。火星も木星も彗星も、私と同様に時間に巻き込まれているからです。そもそも時間のない世界のコンテンツが刻々総入れ替え状態になるという事態が理解しがたいものになっています。
　事実がどうあるか、ではなく、こう見ることも可能だ、ということがすべての科学モデルの性質です。ニュートン力学において空間把握だけを取り上げるならそれは現実に対し矛盾を含むものでしかありえません。時間のない世界を想定しているからそれも自明のことではないでしょうか。空間把握に時間の要素を加えて、初めて現実との整合性を取ることができます。ならば、ミンコフスキー空間のあるべき処理も明らかであって、無時間的とされる光円錐上の出来事も実は時間に巻き込まれる、とすることで現実との比較が可能になるのです。ただ私はそれがいかなる数学的な形になるのか想像できないし、根本的な矛盾を含むものでしかないと思っています。つまりここには時間の因子が既に含まれているので、光円錐が無時間的世界であることを補うためにさらに時間の因子を加えると、時間そのものが立体でなければならないことになるのです。

　ここまでのミンコフスキー座標図に対する私の説明は腹立たしいほど意味不明に違いないでしょう。方程式自体が現実に対応していないから直観的にとらえられない、と私なら結論しますが、科学者の多くは科学的認識のほとんどは直感的に理解できないものだと言うでしょう。では、もう少しわかりやすい例を引きましょう。これもまた相対論の解説書ではよく取り上げられ、かつ直感的に把握することを目的にしたものだからわかりやすいはずです。

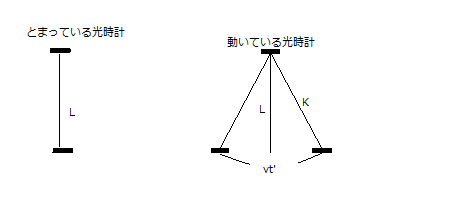
　左図の太線は向かい合わせに固定した鏡です。図の下方から発した光が上の鏡に反射してもう一度下に戻るまでを振り子の一往復とみなし、静止状態の光時計で時間単位のtとします。鏡の隔たりをLとするとこの時計の一単位はt＝2L/cとなります。次にこの時計を右にでも左でもよいから移動させます。光の軌跡を斜辺Kとするとその長さはピタゴラスの定理でK²=L²+(vt’/2)²であり、これでこの状態における振り子の一単位をもとめるとt’=t/√(1－v²/c²)となります。このtとt’はそれぞれ静止した時計、運動中の時計の一単位なので、静止した時計の刻みのほうが速いという事実はミンコフスキー方程式と変わりないものになるでしょう。その割合は　√(1－v²/c²):1であり、もちろんローレンツ変換が長さの変化を求める式そのままとなります。
　光時計を左右の方向に動かしてわかりやすく示したことが、上下左右、さらに斜めの方向へ動かした場合でも成立するということをミンコフスキーの座標と計算式は述べていると考えると全体をつかみやすいでしょう。光時計の場合で言うなら、三角形の斜辺に相当するKはいつだってLよりは長くなるのだから、もし光速度が一定であるなら光がその距離を往復するのに必要な時間は増えるはずです。つまり時間の刻みは間延びします。光時計の移動速度が増すにつれ、三角形は横に伸びてひしゃげた形になります。移動速度が光速度に達すると、振り子の代わりである光は速度の成分をすべてその方向に奪われ、斜めに飛ぶことができません。すなわちこの時計は時間を刻まなくなるでしょう。
　光時計はミンコフスキー空間の仕組みを素人にも把握できるようにファインマンという物理学者が考案したものです。たしかにこれで理解できたと感じるかもしれません。だが何かしらの引っ掛かりも残ります。停止状態の光時計は対面の鏡に向かって直角に光を放っているが、もしこれをスライドさせた場合、右図のように斜めの軌跡として見えるものなのか。また、光時計を上下の方向に動かした時、本当に向かいの鏡に到達するまでの時間は、どちらの鏡から出発した場合でも等しく遅れるのか。