2-10　ミンコフスキー座標の総括　

　繰り返しになりますが、ミンコフスキー座標上では任意の点はデカルト座標と同じ意味を持ちません。意味を持たないと言うのは、デカルト座標では指定された点は「位置」であり、点どうしを結んだ線分は位置の関係であって、点を独立したものとして論じることができますが、ミンコフスキー座標で現実に対応する意味を持つのは原点から引かれた線分のみであり、したがってct軸やx軸もそれだけを取れば有意味でありえるが、その他のことは数学的な意味を持たない模様にすぎない、ということです。一見意味がありそうに見えるが事実と対応していない、という点は、光時計が一定の方向に、一定の速度で動かすときのみ機能することを反映していると思えばよいでしょう。

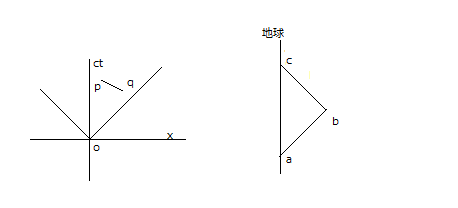
　上図でpやqに原点から線を引くなら意味を持ちます。しかし独立では意味を持つことはできないし、線分pqも無意味です。すなわち何らかの量を表現することはできません。もちろんct軸は自分自身の世界線であり、そこで起こる出来事は他者からの視線を必要とすることなく一様に決まるので、任意の点を選ぶことができます。つまり私が生涯のいずれかの時点でとある出来事に出合い、一週間後に別の出来事に出合うなら、この時間の隔たりと順番は、原点からの視線なのでそのままの意味を持ちます。本当はミンコフスキー座標の中では「私の生涯のどの時点から評価しても変化しない」という意味になってしまっていますが、そこは今のところ問わないことにします。しかしpやqはそうではなく、隔たりの長さどころか順番さえ変わりうるのです。私がある人と路上ですれ違い、この時アンドロメダ大星雲に二人とも目をやるとして、各々の目撃する星雲の姿は数週間規模の時差があるかもしれないと、ペンローズその他がこのことを力説しています。つまりこれは相対論の公式的な世界観です。図に描きいれることは確定した位置を与えるということですが、実際にはそれがあり得ないということが、相対論がこの図に要求する含意なのです。
　もちろん原点が設定されているのだから一つの視点のもとにまとめられているかのようにみえ、私の言い分は極論に響くでしょう。しかし光時計と同様と先に申したような、方向に対する敏感性がこの座標にも存在します。
　右は簡略すぎるがウラシマ効果を表現しており、特に注釈がない場合でもミンコフスキー座標上に描かれているという含意があります。線分ab、bcは準光速の宇宙船が地球を離れ、また戻ってくることを示すものです。この時往路のabをミンコフスキーの流儀で理解するなら、その解釈を帰路に当てはめることはできません。ただしcを原点として改めて設定し、私に向かう世界線として描きなおすことならば可能です。言うまでもないことですが私から出て行く世界線と過去から私に向かう世界線は全く違う性質を持ちます。私の勝手な解釈でこういうのではなく、それが相対論の主張なのです。つまりcbという線分はabの延長として扱ってはならないということです。
　私の世界線すなわちct軸はいかなる外からの視点をも入れる余地はありません。外からの視点を入れるということは無限の多様性を容認するということであり、無意味であって、これは以前に一万隻の宇宙船の例で示したことに準じています。すなわち一万隻の宇宙船がそれぞれの速度でばらばらに散って行ったとすると、私が乗った宇宙船の時間の進み方は、宇宙船ごとによって違って見えるはずなのだから、一万通りの時間が同時に進行していることになり、それは科学として成立しないという主張です。私が参照すべき唯一の時間は、私の時間でしょう。これは誤解されやすい言葉ですが「私の」というのは主観的な時間の流れということではなく、私の持つ時計が唯一の参照すべき時間を刻むという意味になります。
　そしてまた、私が歩く速さを変えただけで、世界の各層の時間の進みが変化すると相対論は主張するのだから、未来の私のある時点で、私が歩いているのか飛行機に乗っているのか、あるいは宇宙船にいるのかわからない以上、ct軸の未来の地点での時間関係は不明というほかはないのです。ただ単に、現在との関係としてその軸が存在するという意味を持ちます。
だがウラシマ効果をこのような単純な図で説明するとき、往路帰路を連続的なものとして扱っている時点で、無限の多様性を入れる間違いを犯していることになります。

　私が地球に残る側、そして知り合いが旅立つ側として、お互い20歳のとき（a）別れたとしましょう。そして彼の帰還（c）が私の時計で10年後だとします。往路を私から出て行く世界線、帰路を私に向かう世界線、と正しく理解するなら、再会の時、私も彼も30歳なのです。奇妙な言い方になりますが、彼が外でどんな年齢の取り方をしようが私の世界線に触れた瞬間に時間の評価はすべて私の基準で書き直されます。つまりミンコフスキー座標で帰路cbを解釈するなら、30歳の時点からさかのぼって計算する形になるのです。しかしbの視点から見ることはできません。
　以上のことが科学に対する無知に起因するかのように言われてしまう可能性を含むことは否定いたしません。あくまで光時計と同様、現実とすり合わせたときに理論からは十分に見えてこない不具合があることを前提とした記述だからです。数学的に忠実ではないように見えるから根本的な誤解がありそうですが、この解釈でも矛盾は生じません。むしろ、これしか解はないと言えます。この考え方ではミンコフスキー座標でのすべての操作は私から見てどうあるかしか表現できないと言っています。ミンコフスキーはそれを「現実そのものである」とみなすことを要求するでしょう。その要求とはもちろんタイムパラドックスとローレンツ収縮です。
　しかしそれは人間の解釈力の問題であって、例の光時計と同様にミンコフスキー座標は一方向にしか有効ではないと私は考えます。相対論とはたびたび述べたように遠近法なのであって、たとえば高速で通り過ぎた球体を傍らの人は楕円形と見る（かもしれない）ということを数学化したものです。すべての解説書の言うとおり、運動する系どうしはお互いが縮んで見えるとしても、系を乗り換えて楕円形を元の球形に戻す作業が禁じられているわけではないでしょう。すなわち、楕円形に見えるが本当は円である、という解が存在します。
　ミンコフスキーの数式は、もちろん相対論のそれも、それ自体で閉じた理論空間を形成しています。つまり、どんなに数学的に詰めて行っても矛盾はないと言ってしまえます。真に論ずべき重要な矛盾とは、論理学者が考えたがるような、ある論理式に内在するものではなく、現実と突き合わせたときに明らかになるものだからです。つまりナンセンスに対するウィトゲンシュタインの考え方や、クリプキの真理値論の奇妙さが暗示するものの中にあります。数学を含む「論理」は、その論理内容だけで外延を指定しつくすことはできない、すなわち解釈を固定することができないのですから。
　単純なデカルト座標であっても事実との対応性を読み取るには慣習の力と読み込みに対する相当に深い知力、もちろん人間は楽にこなすから気づきにくいけれど、想像的知力が必要であろうとは思います。もしミンコフスキー座標での前提を知らずに読み込むなら、タイムパラドックスは生じない可能性もあるのではないでしょうか？
ばかばかしい意見である、との言い分は理解できます。しかしミンコフスキー空間での相対論の展開も、こちらから見ればばかばかしい意見なのです。ミンコフスキー座標で学者たちはわざと間違った解釈を引き出しており、しかもそのことに自覚がないのだ、と言えないでしょうか。
　ミンコフスキー座標で私に向かう世界線、つまり地球に戻りつつある宇宙船は、必ず過去に開いた光円錐（つまり下に口を広げた漏斗状）の内部をたどってくるのでなければならないのです。したがって、どんな形であれ、私の現在に過去から追いついてくるという方向のものでしかありえません。遠ざかるということを私の時間軸からずれてゆくものとして描いた世界線は近づくときは私の時間軸に戻すという作業を要するのです。時間軸がずれながら私の世界線に近づくという概念は相対論が下向きの光円錐で説明する動きに反します。時間軸を戻すというのは単位を一致させて差分を計算するということではなく、過去にまでさかのぼってこの時間軸の基準ですべてを語りなおすということだからです。
　たとえばある粒子が10光年向こうの星から光速の4/5の速度で飛来すると仮定するなら、時間の進みは地球の3/5とみなされ、かつこの距離は6光年です。これは相対論の公式見解通りの計算ですが、シリウス（10光年よりは近いがおよそはその程度）までの距離を6光年とするような記述の本は存在しません。それは光より遅いはずの粒子が光よりも早く到着する（7.5年）ということも含めて、端的にナンセンスだからです。ナンセンスではないとしても、地球基準の時間軸を採用するわけです。ミンコフスキーの式は時間を光に強烈に結び付けすぎて、光の性質が（時間が本来そうであるような）単純な量に対する評価となってしまい、三次元ベクトルであることを忘れています。光時計と同断なのです。もし光をミンコフスキーの主張通りに受け入れると時間のほうが三次元ベクトルを持つことを暗々裏に認めることになり、タイムパラドックスが生じます。光のベクトル性を受け入れるなら、時間は多次元であることをやめ､スカラー量となるでしょう。もちろん光がベクトルなのです。ほかの考え方があり得るでしょうか？
　この考え方は単純な意味での絶対時間を支持するかに見え、気に入らないかもしれません。私は必ずしもそこまでは考えていないのです。遠ざかる物質の長さが縮むことも、時間の間延びも、もし視点から消えるまでを一貫して記述するなら、有効な科学でありうるかもしれません。それが物理学として使い道があるのかどうかはわかりませんし、少なくとも力学が含まれるべきではないとは思いますが。しかしその遠ざかる物質が私の元へ戻ってくるならば、私の時間軸に従います。宇宙船が出発し、帰還するということは、どう考えても客観的世界にとって些少事であって、そんなことで世界の時間軸が変化することはありえないのです。視点の交換による見え方、また見かけと実際のことの関係に対する要求などが二通りの座標は裏返しの関係にあります。デカルト座標で見かけにすぎない時間の遅れがついには解消されるように、ミンコフスキー座標の「現実である」時間の遅れは帰路で解消されるでしょう。つまり、虚構かどうかは問題ではないのです。私は現実ではなく思考の体系について語っているだけかもしれないが、ともかくそこにウラシマ効果は存在しません。現実にもない、すなわち光時計は機能しないと思いますが、あると証明できるならそれを見てみたいものです。簡単なこと、全方向で作動可能な光時計を作ってくれればよいのです。
　最初の仮定として、光時計が作動する方向を持つことを一応受け入れてみました。これはなにを意味するのかというと、１次元の思考であるということです。この限定的な世界の中で、相対論はいかにもうまく働きそうに見えますが、実は矛盾を引き起こします。ましてや、現実の中では矛盾すら生み出し得ない思考ということになります。