高次元宇宙が存在しないなら、ブラックホールは当然否定されます。そしてもう一つ、無限という概念の性質からも否定されます。
　無限大のゆがみとは何でしょうか。例えば一枚の紙を二次元世界と見立てて、それにねじりを与えることがゆがみということになります。このとき、そこに描かれた人がおのれのゆがみを認識できるとしたら、その人はすでに3次元の存在なのではないでしょうか。もとより、ゆがみがあるということですでに3次元が前提とされているということになります。丸めるとか、へこませるとかは3次元の中での行為です。さらにそのゆがみ具合が無限大ということであれば、紙のへこみは3次元を突き抜けたものになるはずで、次元を一つ上げるだけでは足りません。それはどこまで行けば止まるのか。2次元のゆがみは数学的な表現として理解できると同時に現実として把握できるような気がします。3次元のゆがみも同様であると思うのはただの勘違いではないでしょうか。

　無限大の概念を人はなぜかそこにあるものとして考えます。たとえばブラックホールは内部に向かっての無限大の後退速度を持ち、したがって特異点では無限大の重力を持つとされます。無限大の重力とは無限大の吸引力です。これが意味するのは、たとえ数億光年離れた場所であろうと私たちに対し無限大の吸引力として働くということ以外のものではありえません。どんなに大きな力でも十分な距離があれば微弱になる、と考えるのは有限の質量や有限の力でこの問題をとらえているからです。無限大であるとはまさに影響が限定されないということでしょう。特異点という概念だけが、この力が局所的なものであることを理屈抜きで言っています。つまりごまかしているのですが、誰も問題視しません。なぜかと言うに、この部分だけ、重力が「光の脱出速度」に還元されているからです。光が脱出できない領域があり、脱出可能な領域がある。そう言われると、無限大の重力の意味することなど忘れてしまいます。単なる速度であるなら、光速度を上限として次第に弱まるというイメージを簡単にもちうるでしょう。しかしながら、もし太陽が無限大の質量をもち、かつ無限大の重力を持つと考えると、その影響力はやはり地球にとっても同じく無限大であると理解できるはずです。銀河系の中心がよく言われるような大質量のブラックホールであるなら、その重力は我々に対しても無限大であらねばなりません。
　この記述に対して、どうしても無限大ではなく、「とても大きな値」という感覚で対処したくなるのです。すなわち、それでも中心近傍と地球程度離れた場所では少しは違いがあるはずだろうと。しかしたとえ宇宙の果てにあろうと無限大の重力を持つ物体は私たちに無限大の重力を及ぼします。無限大とはそういうことです。なぜなら脱出速度とは重力の強さの指標にすぎず、重力という力そのものは脱出速度プラスなにものかであるはずだから。それはちょうど、虚数を座標上の回転移動だけで語ることが間違いであることと同じです。
　もちろん、空間の移動と重力を同一視する等価原理がまったく正当性のないでたらめ極まる主張であることはあらためて繰り返すまでもありません。すべて論じ方は同じで、重力を脱出速度という条件でのみ発揮できるような環境を作れば等号で結べるような気がするのです。
　二つの誤解、もちろん相対論のほうから見ると私の不理解がここに重なっています。重力の強さを、私の側から重力源へ向かってゆくにつれ次第に増加する力として概念化すると、ついに無限大に至ることがなんとなく思考できます。本当は「非常に大きな力」に到達するだけなのですが。しかし重力源として無限大の力を置き、それがこちらに向かうにつれ逓減すると考えると、いかなる遮蔽物も、たとえ時間という障害であれ、無限大をそれ以下にすることはできないと直感的に把握できるでしょう。ただし第二の誤解が、私は一方通行的だと見る相対論の世界観を双方向的なものであると錯覚させます。お互いが重力源であるのだから、もちろん相互的であるほうがよいのです。しかしここで論じているのは無限大の力を放出するとされるほうに限った話であって、双方向的であることはむしろ論点ずらしでしかないと非難される恐れがあります。この論じ方は私が殊更恣意的に持ち込んだものと言えば言えるでしょう。
　すなわち、重力の脱出速度への還元です。光速度という上限が決まっているのだから、ここに無限大の入る余地はありません。光速度に等しい脱出速度は単に定義上無限大と同様のふるまいとして理解されます。しかし重力は加速度そのものではありません。一定の状況下において、加速度として扱えるというだけのことです。脱出する必要のない物体であれば速度の計算は必要ありません。

　イメージのみに頼った理屈がもうひとつ、重力は空間のゆがみであるということから生じます。それは下図のような形で理解することです。

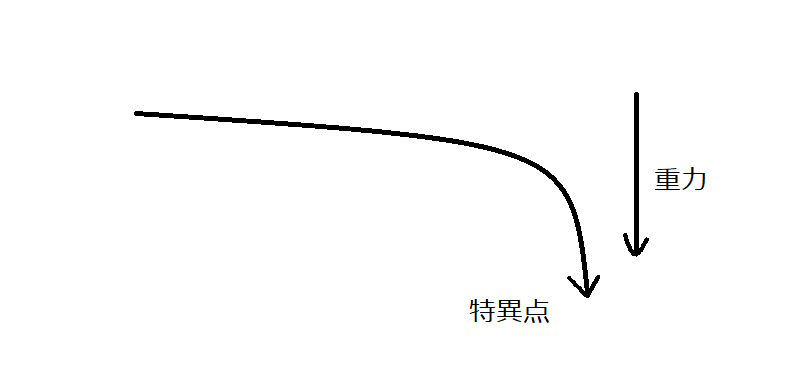
　ブラックホールから遠い領域について、重力は平坦なもののごとくに描かれますが、近づくにつれ急激に奈落を目指す形になります。これは大変もっともらしいイメージですが､相対論は常に相互的なものであるとすれば、この奈落の底から我々を見る視点も当然あるはずなのです。つまり、あちら側からは私たちの存在がブラックホールでなければならないということです。私たちはまさにブラックホールに飲み込まれつつあり、時間が無限に伸びゆく瞬間を経験しているなどとまじめに論じる学者もいるようですが、彼は一体何をブラックホールと目するのでしょうか。多分、何か抽象的な虚空を思い描いているのでしょうが、実は太陽かも知れないし、地球かも知れない。私の目かも知れないし、私の細胞一つ一つかも知れない。本当はすべての存在がブラックホールであると言うしかなくなるのです。なぜなら銀河系の中心部が無限大の重力を持つなら、その特異点から見ると銀河系のすべての部分、いやそれどころか宇宙のすべての部分が特異点になるからです。相対的であるとはそういうことなのでしょうから。（註1）

　たとえばブラックホールは超大質量の恒星のみが生涯の終わりにたどり着く特殊な天体とされます。恒星の外郭というのは、中心部で数万度から数億度にも達する高温のせいで外側にはじけようとする圧力と、内側に戻そうとする重力とが均衡する地点で大きさが決まります。小さな質量の星は中心部の温度が上がらず、ゆっくりと燃料を消費し、大きな星ほど早く燃えます。時間の長短はありますが、生涯の大部分を安定した状態で過ごした後、あらかたの燃料を使って内部温度が保てなくなると収縮が始まります。最初は固体化し、そこを過ぎると原子がぎちぎちに詰まる状態になるわけなので、通常ならどこかで止まるはずです。どこで止まるかは重力とのバランス次第であり、元の恒星の質量で単純に決まるでしょう。結果が白色矮星であったり中性子星であったりするのですが、それらは従来の物質というイメージに沿ったものです。極端に大きな恒星は重力が圧倒的に勝ってしまうので、無限に収縮する状態に入ってしまいます。
　相対性理論の相対性とは、単純に理解するなら、違う世界線の住人は、一つの物理現象に対し、違う結論を出すということです。見やすい例として、高速で移動する相手は縮んで見えるという現象を取り上げてみましたが、それと同様に、高速で移動する物体の質量が増えるということはすでに現代科学の常識とされています。これはガリレオの相対性にもニュートンの体系にもない考え方です。質量は変わらず、速度の上昇分だけ、物にぶつかったときの衝撃度や、速度を緩める際に使う力が増えるという考え方をします。相対論だけが、質量そのものが増えると言うのです。
　ところで、速度は相対的であるという前提を考慮するに、私が見てブラックホールを形成するのに十分な質量のある星でも、別の観測者には軽すぎると見える場合があるでしょう。その逆ももちろんあります。宇宙のすべての恒星について、ブラックホールを形成するに足る質量を持つとみる観測者がそれぞれ存在するはずなのです。何しろ全銀河はものすごい速度でお互いに遠ざかりつつあるというのですから。地球のような小型の天体でさえ、見る人の速度によっては、銀河系に匹敵する質量を持つと、相対論の計算上はみなされ得ます。恒星ではなくとも、それだけの質量があればもちろん重力に負けてしまうでしょう。しかし上記のような話は全く聞いたことがありません。ブラックホールは問答無用でブラックホール、地球は固体としての地球です。ではいかなる特権的な視点がこの質量を決めているのでしょうか。これは非常に大きな謎で、しかもすぐに誰の頭にもよぎりそうであるのに、これを扱った論文というものを私は見たことがありません。
　私の考え得る唯一の理由は、結果論として決まっている、というものです。白色矮星がそこにあるのだから、そのことに疑問をさしはさまず白色矮星として扱う、という具合に。大変失礼ながら、思考停止しているのではないか、ということです。
　私が相対論を信じないからこういう疑問が起こるのであって、信じていれば疑問にはならないのでしょうか。しかし別の銀河の住人は我が銀河の白色矮星をブラックホールとみる、ということが相対論をまじめに受け止めた結論になるのではないか。それは、私たちの見ているゾウリムシが、高速移動者にはシロナガスクジラに見えるというのと同じくらい、変な話です。相対論がこの疑問を無視してよいはずはありません。
　というのも、それ自体で静止状態、運動状態と決めてしまうことができない、ということが相対論の大きな柱だったはずだからです。つまり絶対的な質量や運動量は存在せず、視点との相関関係のみが、これらの量を決めます。星の質量が相関関係で決まるということであれば、私には白色矮星と見える当のその星が、当然別の相関関係を持つ観測者にはブラックホールに見えることも認めなければなりません。これが相対論の正しい解釈であって、私が論外のたわごとを垂れ流しているわけではないと思いたいのですが、ことが明白すぎてかえって自信がなくなります。
　相対論の支持者たちは速度やゆがみの度合い、重さなどといった量的な差だけを取り上げたがりますが、世界のすべての局面において、量的な差は質の違いに直結しています。私たちの太陽が、とある星系からはベテルギウス並みの重さに見えるとしたら、もうとっくに星としての生涯を終えているはずなのです。重く見えているが、事実は現状の太陽のとおりである、ということも肯定するのなら、重く見えるということは理論関係ではなく「単にそう見える」ということであって、重いということから帰結する物理学上の事実は何一つないということもまた認めるしかありません。つまり白色矮星がそこにあるのなら、相対論でそれをどう見るかということは関係なく、軽い星なのです。

　質量が増えるということを単純に注目すると、見えにくいことがあります。質量が増えるとする視点が、一つではなく本当は無数にあるということが相対論にすっぽり抜け落ちている部分であるという部分が、実はもっと問題であると思われるのです。
　双子のパラドックスという有名なパズルがあります。それを検討することは後回しにして、ここではそれが兄と弟、たった二つの視点で語られていることに注意を喚起しておきます。相対論は常にこの語り方をします。列車の内外の人、縮む運動体を外から見る人と内部の人。しかし実は一対一の関係とみなすからパラドックスのように見えるのであって、一対無限であることを理解すれば、「一対一」のどちらかの一は全く釣り合わない１/∞であることが明らかになるのです。
　地球が危機に陥り、数百万の宇宙船が、それぞれでたらめな方向に、速度もばらばらに散って行ったとします。それぞれの時間の流れ、ローレンツ収縮はどの船から見るかで極端に変わります。私がその中のひとつに乗っているとして、私の時間の流れは、各宇宙船の視点だけでも数百万の正解があることになるでしょう。そのうちのどれを選べば「私の正しい時間の流れ」なのか、決める手段はあるのでしょうか。私の知らないうちに、さらに後発組の出航があったとしたなら、私の感知しないところで私の絶対時間が左右されることになってしまうのでしょうか。
　取りうる視点の数が無限であるのだから、私たちは自分の時間をひとつの絶対量として尊重するということが、まずは当たり前で常識的な判断です。すなわち、私の1時間は、相対論によればこれを外から眺める視点によって、0から無限大まで変化し得ます。では外から眺めるということに科学的な意味を与えることはできないのです。なぜなら0から無限大までの任意の内的時間に対し、いずれも客観的な裏づけがあるということになってしまうのだから。しかもそのすべての解は光速度の絶対性に導かれたものです。つまり相対論ではすべて正しいということなのです。これは時間の主観的な見方と客観的な見方の対立などという類のものではなく、意味のある表現ができないという単純な事実でしょう。はっきり言って、ナンセンス以上のものではありません。
　もし宇宙船という不安定なものを説得力として不十分に感じるなら、それらが広い宇宙の遠い銀河にまで行って、てんでに住み着いたと想像してもよいのです。私たちはどの宇宙船を選んでも、特に不都合なしに時間を消費し、行き着いた銀河で惑星を探し、細々としかし希望を持って新たな環境づくりに取り掛かるでしょう。時間が進むのが遅すぎて仕事にならないとか、手に持った器具が縮んでしまったとか、そんなばかげた事態にはならないはずです。ではそこで故郷の銀河系を振り返って、まだそこにいる人たちの様子が仮に見えるとして、自分たちの生活のテンポがおかしいと気づくことになるのでしょうか。そうではなく、まあありうるとしてですが、銀河系に残った人たちの時間は間延びしているように「見える」と言うのではないでしょうか。これは遠くにあるものが小さく「見える」ということと同じ構造に思えます。
　それで初めて相互的であることの意味が理解されます。遠くの銀河の生物は私たちから見て間延びした時間とローレンツ収縮の中にいるのだし、逆に彼らから見ると私たちのほうが間延びした時間とローレンツ収縮を体験しているということは、そのままでは極めて不条理な言い分です。しかしこれは解くべきパラドックスなどではありません。単にそう見えるだけで事実は違う、ということです。相対論はそう見えるだけのことを真に受けて、事実としてそうなっている、と言ってしまいます。大変滑稽な間違いです。そのうえ、「そう見える」だけの視点は無数に想定できます。
　世界全体を等質なものとして見渡せる場所は存在しない、という相対論の言い分は、大変正しそうに響きます。したがって「私にはこう見える」という意見の押し付けも正しく思えてしまいます。しかしニュートンは神の視点に居座って絶対時空を論じているのではなく、いちいちその場に足を運んで同じ視線のもとに見るよう促しているだけなのです。その結果、遅かったはずの時間は正常な進みであることがわかり、縮んでいたと見えた相手の物差しの目盛はふつうであることがわかり、重くなっていると思われた質量は実は変化がないと知れるのです。

　註1　無限の後退速度、という概念については第二部に譲ります。相対論は光の速度を実際の無限大ではなく、名目上の無限大としました。それにもかかわらず、実際の無限大として扱ってしまったことがブラックホールという途方もないたわごとを生む原因なのですが、タイムパラドックスを解く過程の中で論じた方が理解しやすいと思います。