2-９　光時計は作動しない　

　光時計のことで、一応の説明を付加しておく必要があるでしょう。進行方向に直角の向きに光を飛ばしたとして、光は斜めに行くわけではないという意見があり、行くという意見もあります。ここは、有名なマイケルソン・モーリーの実験の評価、あるいはブラッドリーの光行差現象の解釈を含め、かなりかまびすしい意見のやり取りがあります。もちろん相対論に賛成の人なら当然斜めに飛ぶことを支持します。
　しかしこの場合の斜めに飛ぶとは実際にどういう意味なのでしょう。光時計考案者の意図では「光時計という独立した運動系の空間内のことであるから、その空間の移動に沿った動きをしている」ということになるでしょう。
　しかし現実の現象として考えた場合、光を数学的な直線として発射することはできません。日常的な光源を考えた場合には四方八方へ拡散してゆく状況を簡単に想像できます。それならば直角にも行くし、斜めにも行くことになります。もし光をピンホールで絞ったとしても、もちろん幅はあります。
　奇妙なことに、レーザー光のほうがはっきりと進行方向に傾いた、斜めの飛び方をするという報告があります。レーザーとは、とても非科学的なたとえで言うなら、でたらめな動きをするたくさんの球状のものを細い筒に流し込んでやって、球はあっちこっちぶつかり合いながら結局は一方向の流れとして出てくるような仕組みです。この筒を横向きに動かすなら、中の球のぶつかり合いに何らかの影響があるだろうことは理解できます。したがってレーザー光が、装置の進行方向に沿った斜めの飛び方をすることもあり得るでしょう。
　反相対論の側はおおむね、進行方向へ傾いた光の飛び方を認めません。だから斜めにも飛ぶことを持って、相対論支持者は「やはり相対論が正しかった」といいます。しかしそうでしょうか。レーザー光の場合には装置の人工的な作りが斜めの光を生むのであり、相対論とは何の関係もありません。そしてそれ以外の光の場合、むしろ相対論は否定されたと考えることもできてしまいます（もちろんこの段階でそこまで言ってしまうと、また言いすぎになりますが）。なぜなら、もう一度光時計の前提を考えてもらいたいのですが、向かい合わせの鏡に囲まれた空間が運動系という異空間であるから、そこを実はまっすぐ飛ぶものとして想定される光が、空間外からは斜めに飛んだように見えるという設定なのです。しかしここで持ち出される光の軌跡は、レーザー光含め、ことごとく外と一体となったオープンな空間内の出来事となっています。では、それは相対論の効果を証明するものではないでしょう。
　反相対論が「光は斜めに行かない」というとき、それは空間の移動による光の変化はない、という原理論を指摘するのであって、現実の、いわば不確定の部分が演出する光の軌跡の変化を言うのではありません。混同してはならないところです。
　そして大事なことは、斜めに飛ぶかどうかではなく、斜めに飛んだ光とまっすぐの光の時間的長短のはずではなかったでしょうか。そしてもう一つ、これは特に書いておかねばならないことですが、エレベータの思考実験において、無重力空間内を引っ張り上げる箱の内部で、床に平行に打ち出される光は下向きに曲がっているかのように見えるとアインシュタインが言っているのです。すなわち、光はエレベータの動きにしたがって斜めに行くのではなく、全く外からの視点で直線的に飛ぶと彼は言っており、それを相対論の基礎としているわけです。あまりにもご都合主義すぎるというべきではありませんか。

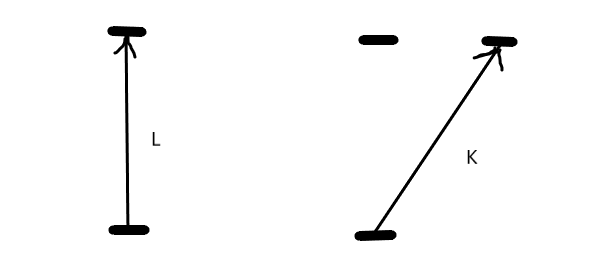
　つまり、上図において、下から発せられた光Lが、向かい側の鏡に当たるはずのところ全体が速度vを持って右に移動しているので、「相対論効果によって」Kの軌跡を描くことになってしまったのか、あるいは最初から移動後の鏡めがけて飛んでいた光だったのかは関係なく、時間のひと刻みとしてK=Lとなるかどうかということではなかったでしょうか。
　すると相対論の側は重大な錯誤を犯していることになります。つまり、相対論の主張する「光がちゃんと斜めに飛ぶ事象」はすべてオープンな空間の事例を出してしまっている。ならばK=Lが成立するということは、速度の違う二つの光を私たちは目撃しているということになり、それを相対論の側から言い出してしまったことになるのではないか。

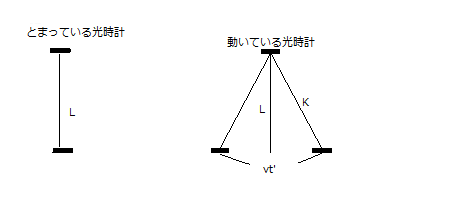
　原理論として、ふたつとも素人考えの引っ掛かりのほうが正しいのだ、ととりあえずこちら側の主張を述べておきましょう。光時計の図は光に慣性の法則が働くかのような描き方をしています。あるいは目の前をよぎる電車の窓から明かりがこぼれており、それを目で追うときの印象でとらえられています。しかし私が見る窓の明かりはまっすぐ私に向かってきたものであり、横向きに飛んだ光を見ているのではありません。電車が左から右へ滑ってゆくとき、視界の左右で同じ光源を見ているのであっても、とらえた光は違うものです。つまり左図の鏡時計をかなりの速さで動かしてやったなら、光が反対側に到達するころ、その場に鏡はすでにないでしょう。移動後の鏡に当たる光は、最初からその方向を目指していた斜めの光である、と考えることが正しいように思われ、それならば長い距離を移動する分だけ時間がかかる、と考えることが妥当ではないでしょうか。しかし相対論に批判的な側がこだわるこの点について、私はそれほど重要視するべきではないという気がしています。直進するはずが斜めに飛ぶ、という理屈が相対論なのだから、その点をいくら言いつのっても聞く耳は持たないはずでしょう。
　むしろこの時計を（図で言うと）上下の方向に動かすとき、時の刻みは一定ではありえない、ということを考えてみるべきかもしれません。左図において、自分が時計の下方にいて遠ざかるところを眺める形とすると、光は遠ざかる動きと近づく動きの繰り返しになります。この際に光が一定の速度に見えるためには、光の往復の動きに伴って時計本体が伸縮、もしくは速度の緩急を繰り返すことになるでしょう。時計と光がともに遠ざかるとき、鏡は逃げる形になるので、光はより長い距離を飛んで向こう側に着くことになり、もしこの時計と一緒に移動する人があれば時間の進みは遅くなります。光がこちらに来るとき鏡は迎える形であり、短い移動で済むはずなので時間の進みは早まるでしょう。第三者の立場の私と時計とともに移動する人の、どちらの視点でも光速度一定の条件を満たし、かつ時計が安定しているための唯一の条件は、それが静止しているとき以外にはないことになります。
　光がジグザグに飛ぶ形で動いている合わせ鏡の時計の場合、時計の内部と外部からの視点で時間のずれ具合は常に一定であり、私たちをだますのに都合の良い形でした。しかしこちらは不安定極まりないどころか、時計の内外での視点の違いは光の移動距離を変化させません。ジグザグ型に飛ぶ場合と同様の間延びを与えようと思うなら、時計が進行方向へ動く速度を光の速度に上乗せしてやればよいのですが、もちろんこれは相対論が禁じていることです。

　光時計とは向かい合わせの鏡のあいだを往復する光を振り子代わりにした時計でした。例えば列車の天井と床を鏡張りにし、床から発した光が天井に当たってもう一度床に戻る一工程を単位時間とするようなものです。相対論の主張ではこの列車が止まった状態でも、走っている状態でも、光の往復する時間は変わりません。走っているとき線路わきでこれを見る人には光がジグザグに飛んでいるので、明らかに光が飛ぶ距離は増えるはずですが、かかる時間は同じである、とされます。
　ところでこの時のジグザグの軌跡は、列車の中で毬つきをする場合の毬の軌跡そのままであることに気づきます。静止状態の地面と同様にボールを使って遊べるのは、言うまでもなく列車の移動がボールに進行方向（この場合には横向き）の力を与えているからです。列車内で進行方向に沿ったキャッチボールが可能であるのも同様の理屈ですが、こちらは時計を上方向へ移動させることに対応します。光時計が考案者のもくろみ通りに時を刻むという根拠は、この日常的体験を漫然と反映しているだけのことではないでしょうか。どの方向への移動にせよ、時計自体の移動速度を光の移動速度に足し合わせることでのみ、まともに作動するという結果が成立するのですから。
　だがこれは光時計の意図と微妙に違っています。光時計の場合には、上の例でいえば列車内が完全な独立空間であり、外からの力を全く遮断するから、その空間の移動に沿って光も斜めに飛ぶという設定になっているわけです。しかし光時計として出される説明は、この例に従うなら常に等速で直進する列車をモデルにしています。それでよいのでしょうか。たとえば、等速で直進中の列車の中でのキャッチボールはスムースにこなせるでしょうが、加速中にはそうはいかない。曲がるときもそうです。ボールは列車に取り残される方向へ曲がります。
　光時計は曲がりなりにも時計なのです。静止中と等速直進運動の下でのみ、一定の刻み方をするなどと言うナンセンスな代物であってよいはずがないでしょう。ここで相対論側の言い分は、光は空間の移動によって、それに沿った進路を取っているのだから、キャッチボールのボールとは別の理論になるということでしょう。だが物で囲った内部が物理的な意味で別空間にはなり得ないことは現実問題としてあまりにも明瞭です。
　せっかく列車を光時計の見立てとして出したのだから、このまま続けると、列車を外界から全く独立した、いわば閉鎖空間とみなすことでこのシステムは成立します。「移動する列車と同時性の問題」で見たとおり、すべての物理現象がこの内部空間のみで完結し、まわっているものと見なしているのです。でも、そういうことがあり得るものでしょうか。ホームで列車に乗り込み、出発の瞬間、私たちは立っていれば足の裏、座っていれば椅子に預けているお尻や背中に衝撃を感じるでしょう。加速すれば、全体に引きずられる感じだったり押されている感じだったり、とりどりに体の感覚を味わうことになります。しかし列車内が物理的に自立した異空間であるなら、私たちはその「空間」の動きと一体化するのであって、床や背もたれからの微細な力の変化を示す信号はむしろあり得ないことなのではないか、との疑問が生じます。
　運動系という不思議な空間は存在せず、地面という静止系の上を列車という物体が移動し、その列車の中に人がいる。つまり車内の人は列車という運動系ではなく、地面という静止系の上に、間接的にではあるが、紐づけられた存在として考えなければ、全体をきれいに語ることができないのではないでしょうか。発車や加速度を知ることができるということは、結局それが正解なのではないでしょうか。
　私たちは車窓から外の景色を眺めることができるし、外の音も聞こえます。外から中の様子もうかがえます。ここまで、いろいろな物理的事象を連続的に語ることができる空間で、時間の因子だけが独立し得ると、そんな不思議なことがあり得るものでしょうか。
　これは列車をもっと閉鎖空間的な、例えばコンテナに替えても同じことです。トレーラーが妙な加速をすれば、中の荷物は崩れます。光時計も、要するにコンテナと同じです。内部が別次元の閉鎖空間になっているわけではありません。
　静止中のモデルならいざ知らず、移動中の光時計は、正確なモデルを作ることが不可能なのだと思います。そのことは相対論支持者の側もうすうす気づいているらしく、いくつかの案をネットや書籍で見かけました。その中には風変わりなもの、たとえば完全な球体の内部を鏡にしてその中心にセンサーを置く、等々もありましたが、加速や方向転換などといった不意の状況変化をうまく解決できるものは見つかりませんでした。大雑把にとらえると、どのモデルでも往路復路ともに光速度一定の条件を満たすために、光をベクトルではなく単なる変数とみなしています。ファインマンの出した元の案がまさにそういうものでした。単なる変数とみなす簡単な方法は往復を個別に考えずに、一プロセスとみなして平均をとってしまうこと、もしくは振動数に置き換えてしまうことです。要するに、空間においてみた場合の思考を放棄して、単純な式のみで考えようとします。
　光時計は素人向けにわかりやすく概念化したものであるから時空の現実を反映できていない、とするのも一つの考え方でしょう。これだと、ミンコフスキーの、より抽象的な形が正解であることになります。もし時間の遅れがあるなら、どの方向に動かそうと光はゆっくり進むはずなので、現実的で直観による把握が可能なモデルの提示が必要であると私は思いますが、そうではないと言う人がいることは理解します。ただ、ミンコフスキーの方程式と座標は、実は4次元時空の多様性を表現できておらず、現実の光時計が方向に対してまったく無関心であることと同様の誤りが潜んでいるとしたらどうでしょう。ミンコフスキー方程式はどの方向へ進ませたときでも正常に作動するかのように記述される光時計の考え方で組み立てた数式（ローレンツ変換のあれ）を、全方向で通用するものとして書き換えただけのものであり、いわば数学上のトリックにすぎないのではないでしょうか。